Statistical Power
There are five specific empirical components that affect statistical power in applied research
Statistical power is the ability to detect significant effects, given that they actually exist in the population. There are five specific empirical components of statistical power that come into play when designing a research study. All five components have interdependent relationships with each other that greatly influence statistical power. The decisions made by researchers for each of these components drastically impacts statistical power.
Here are the five empirical components that influence statistical power:
1. The scale of measurement of the outcome
2. The research design
3. The magnitude of the effect size
4. The variance of the effect size
5. The sample size
Researchers can increase statistical power by measuring for continuous outcomes (increased precision and accuracy in measurement), using within-subjects research designs (each participant serves as their own control), hypothesizing large effect sizes with limited variance (large and homogeneous effects are easier to detect), and collecting a large sample size (there is a strong positive association between sample size and statistical power). Conducting an a priori statistical power analysis is an important part of planning any study.
Here are the five empirical components that influence statistical power:
1. The scale of measurement of the outcome
2. The research design
3. The magnitude of the effect size
4. The variance of the effect size
5. The sample size
Researchers can increase statistical power by measuring for continuous outcomes (increased precision and accuracy in measurement), using within-subjects research designs (each participant serves as their own control), hypothesizing large effect sizes with limited variance (large and homogeneous effects are easier to detect), and collecting a large sample size (there is a strong positive association between sample size and statistical power). Conducting an a priori statistical power analysis is an important part of planning any study.
You can read below for a discussion about statistical power or click on the Statistical Power button to continue.
Statistical Power and Isomorphism
Statistical power is a nebulous statistical construct that many researchers admonish in favor of asking, "How many people do I need to find statistical significance?" In its most basic operationalization, statistical power is the chance one has of detecting a significant effect, given that the effect actually exists in the population of interest.
Or, continuing with the question above, a power analysis will tell you "how many people you need in your study to find a p-value below .05!"
Conducting an a priori statistical power analysis is an integral part of planning any study. Running an a priori power analysis gives researchers an idea of how many observations of the outcome will be needed to detect a clinically meaningful effect.
One potential framework for understanding statistical power is grounded in the phenomenon known as isomorphism. Isomorphism can be defined as the systematic interdependency between empirical constructs. A change or decision made in one empirical area will always cause a predictable and logical change in the other associated constructs. The sample size, the scale of measurement of the outcome, the choice of research design, and the magnitude and variance of the effect size each affect statistical power and each other in a predictable manner. There are some fundamental principles that explain the isomorphic tendencies between the five components of an a priori power analysis:
Or, continuing with the question above, a power analysis will tell you "how many people you need in your study to find a p-value below .05!"
Conducting an a priori statistical power analysis is an integral part of planning any study. Running an a priori power analysis gives researchers an idea of how many observations of the outcome will be needed to detect a clinically meaningful effect.
One potential framework for understanding statistical power is grounded in the phenomenon known as isomorphism. Isomorphism can be defined as the systematic interdependency between empirical constructs. A change or decision made in one empirical area will always cause a predictable and logical change in the other associated constructs. The sample size, the scale of measurement of the outcome, the choice of research design, and the magnitude and variance of the effect size each affect statistical power and each other in a predictable manner. There are some fundamental principles that explain the isomorphic tendencies between the five components of an a priori power analysis:
Categorical outcomes DECREASE statistical power and INCREASE the needed sample size. This is due to less precision and accuracy in measurement.
Ordinal outcomes DECREASE statistical power and INCREASE the needed sample size. This is due to less precision and accuracy in measurement.
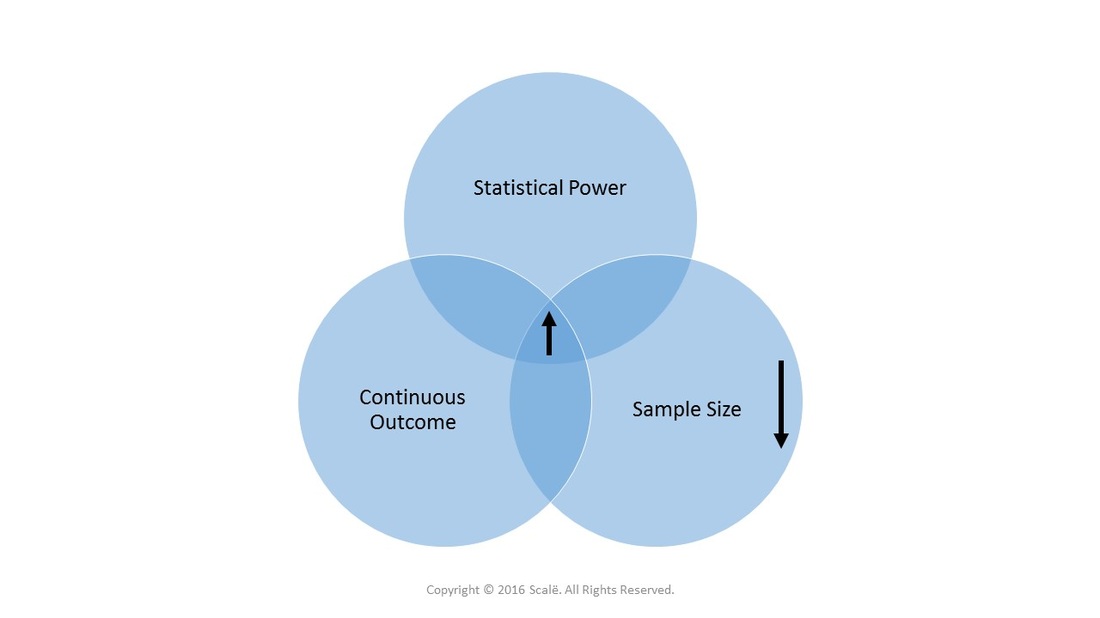
Continuous outcomes INCREASE statistical power and DECREASE the needed sample size because of more precision and accuracy in measurement.
Between-subjects designs DECREASE statistical power and INCREASE the needed sample size. More observations of the outcome are needed to compare independent groups on an outcome.
Within-subjects designs INCREASE statistical power and DECREASE the needed sample size. Each participant serves as their own control.
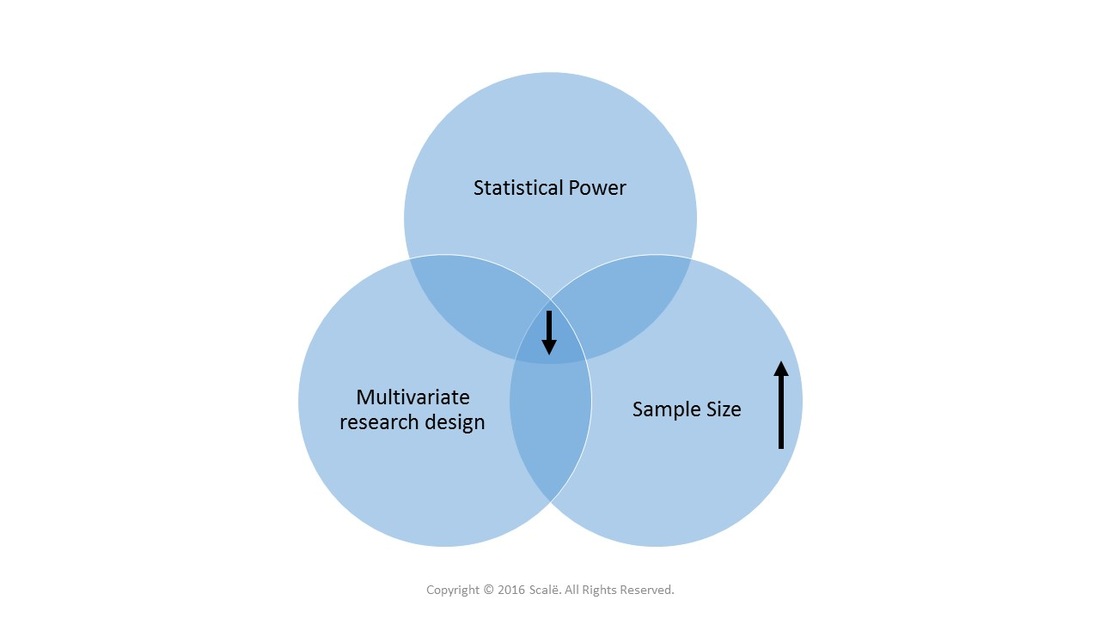
Multivariate designs DECREASE statistical power and INCREASE the needed sample size. More observations of an outcome are needed to detect confounding effects of various demographic, clinical, prognostic, and predictor variables on outcomes.
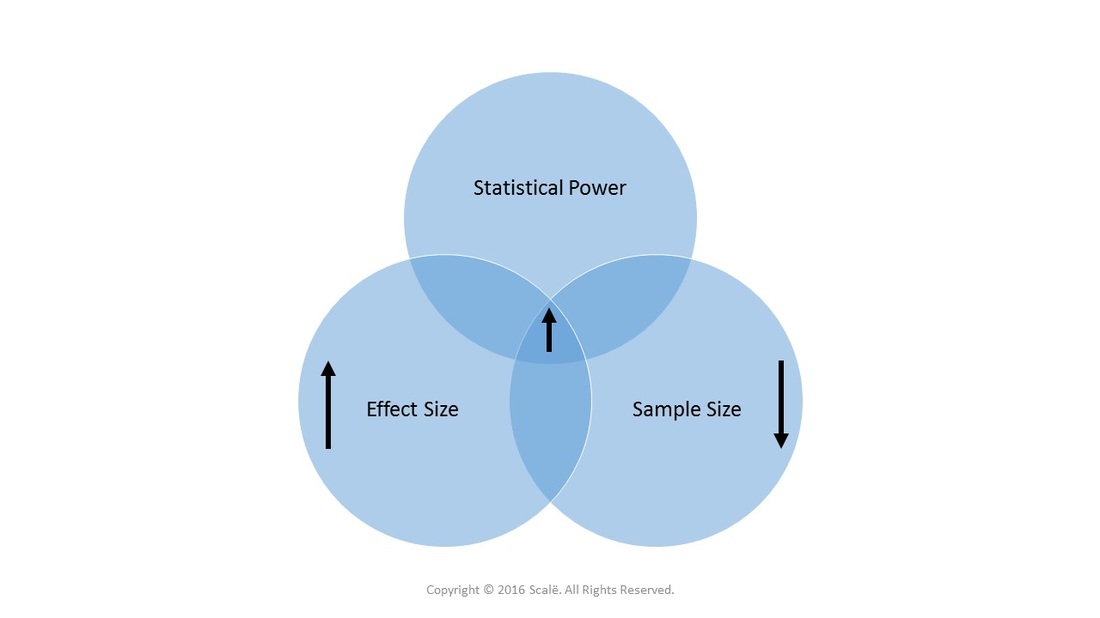
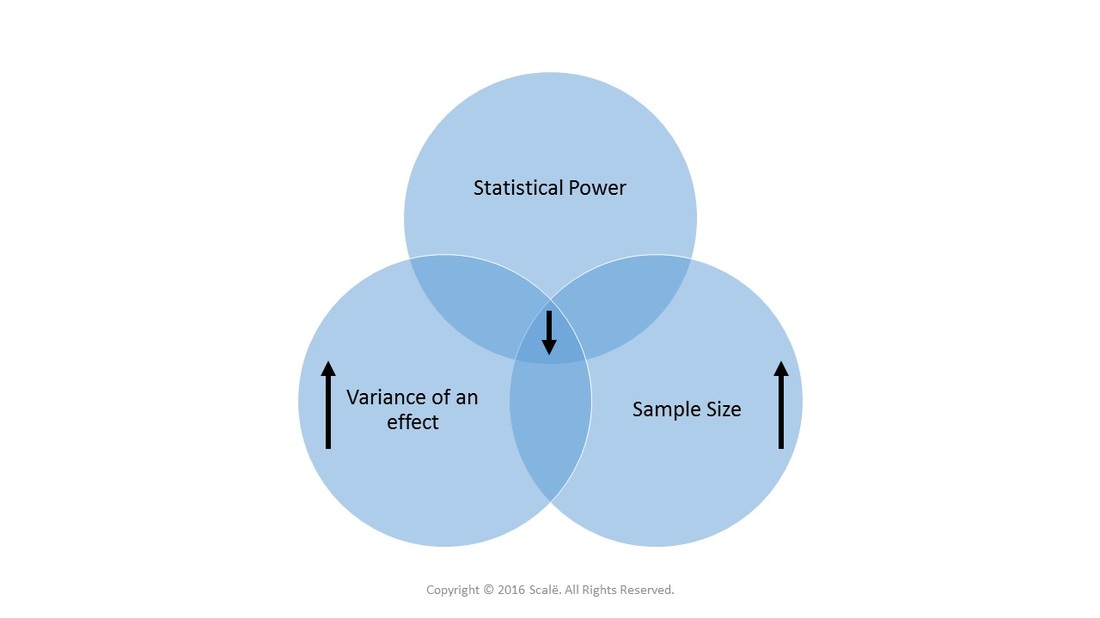
Large effect sizes lead to SMALLER sample sizes and INCREASED statistical power. Large effect sizes are easier to detect.
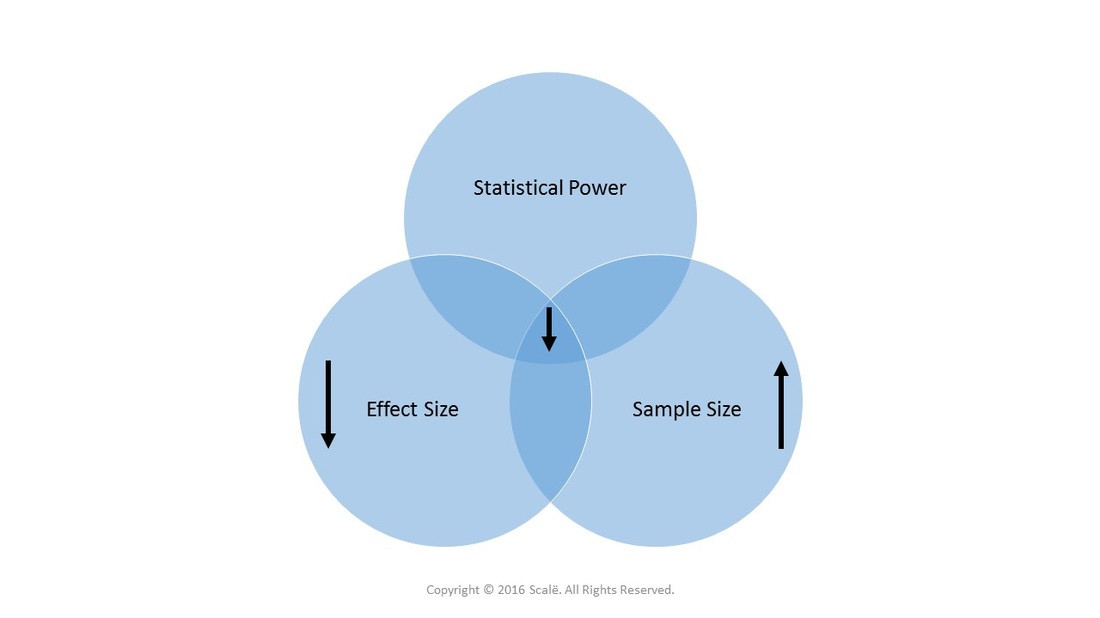
Small effect sizes lead to LARGER sample sizes and DECREASED statistical power. Small effect sizes are harder to detect and therefore require more observations of the outcome.
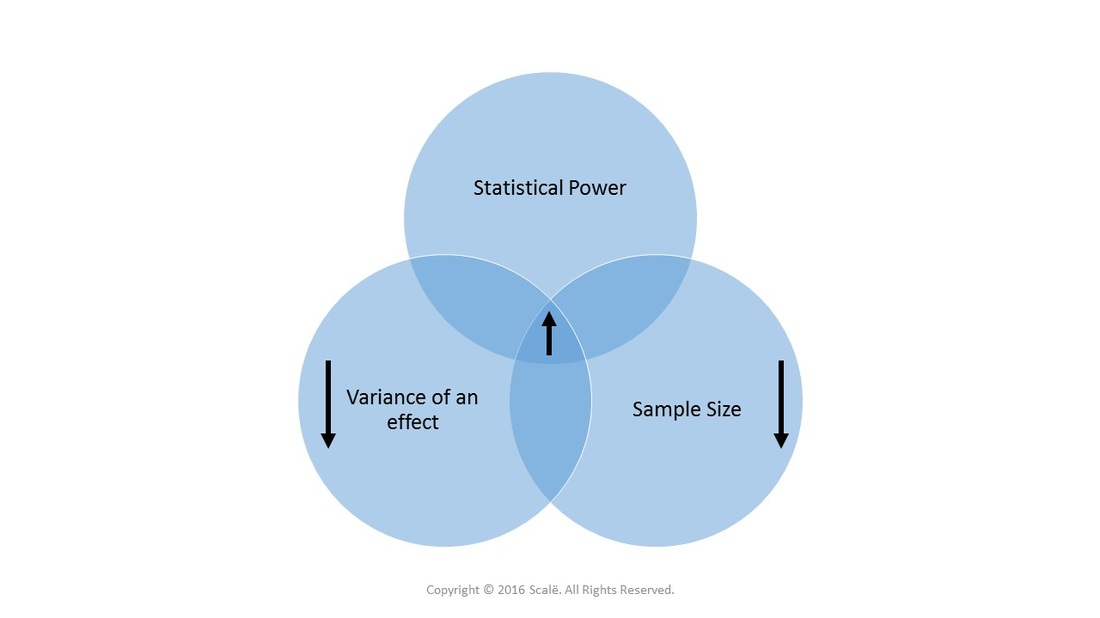
LIMITED variance in the outcome leads to INCREASED statistical power and SMALLER sample sizes. Homogeneity in a distribution means groups will be well differentiated in regards to outcomes.
EXTENSIVE variance in the outcome leads to DECREASED statistical power and LARGER sample sizes. Heterogeneity in a distribution means groups will not be well differentiated and will overlap in regards to outcomes. More observations will be needed to find actual differences.
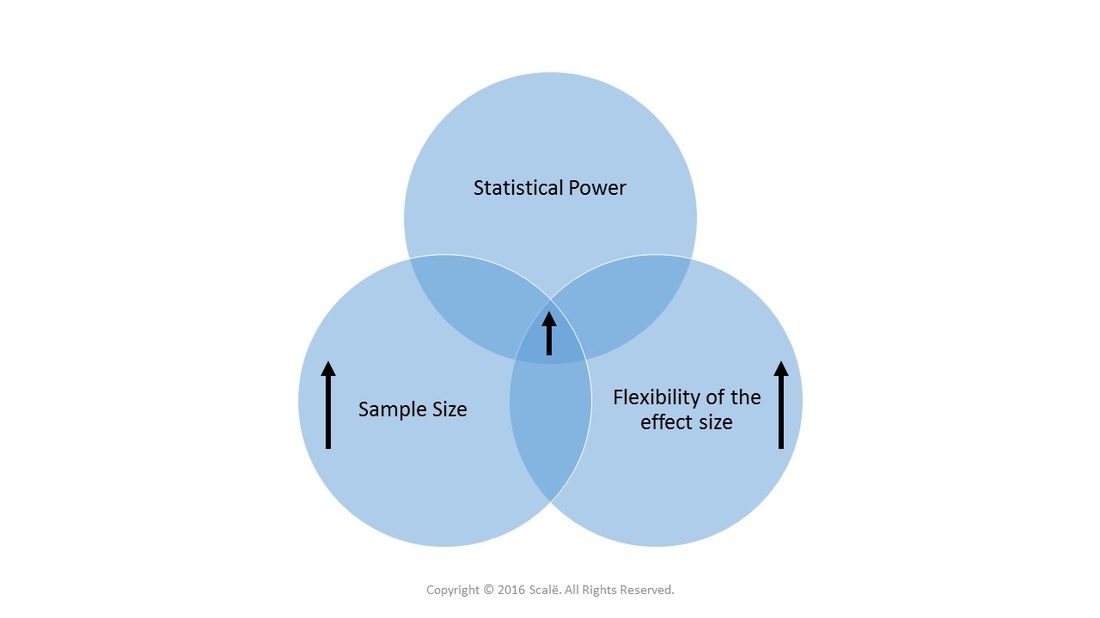
Large sample sizes lead to INCREASED statistical power and INCREASED flexibility of the effect size.
Flexibility means being able to detect both small and large effects, regardless of limited or extensive variance.
Flexibility means being able to detect both small and large effects, regardless of limited or extensive variance.
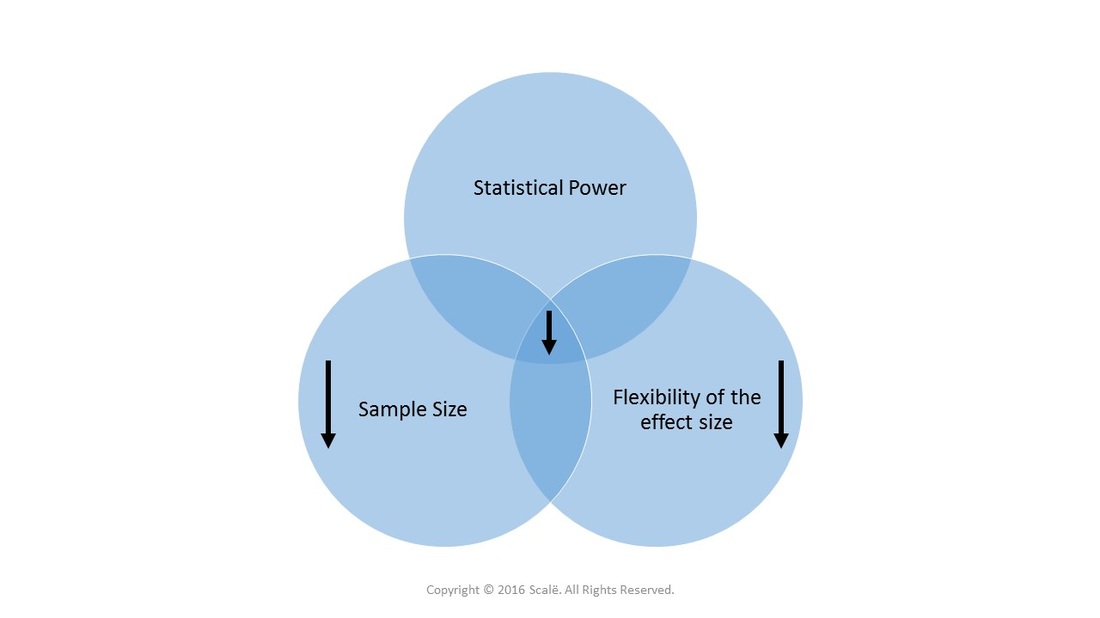
Small sample sizes lead to DECREASED statistical power and DECREASED flexibility of the effect size.
Flexibility means being able to detect both small and large effect sizes, regardless of limited or extensive variance.
Flexibility means being able to detect both small and large effect sizes, regardless of limited or extensive variance.
Click on the Statistical Power button to continue.
Hire A Statistician
DO YOU NEED TO HIRE A STATISTICIAN?
Eric Heidel, Ph.D., PStat will provide you with statistical consultation services for your research project at $100/hour. Secure checkout is available with Stripe, Venmo, Zelle, or PayPal.
- Statistical Analysis on any kind of project
- Dissertation and Thesis Projects
- DNP Capstone Projects
- Clinical Trials
- Analysis of Survey Data