Multinomial logistic regression
Test multivariate associations when predicting for a polychotomous categorical outcome
Multinomial logistic regression is the multivariate extension of a chi-square analysis of three of more dependent categorical outcomes. With multinomial logistic regression, a reference category is selected from the levels of the multilevel categorical outcome variable and subsequent logistic regression models are conducted for each level of the outcome and compared to the reference category. Adjusted odds ratios with 95% confidence intervals are reported for inferential purposes with multinomial logistic regression.
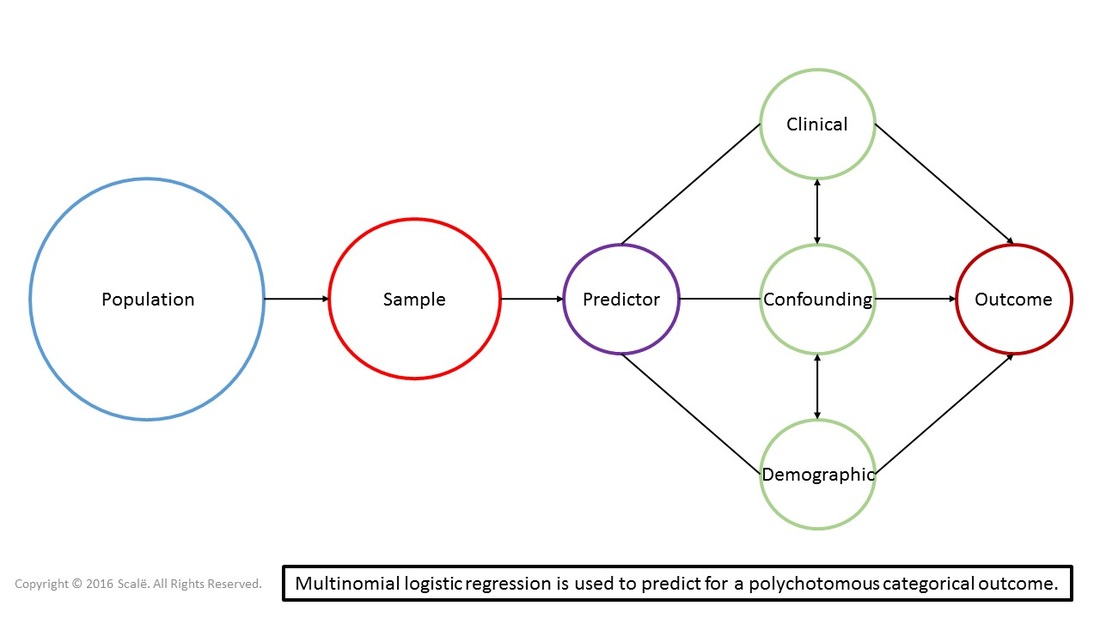
The figure below depicts the use of a multinomial logistic regression. Predictor, clinical, confounding, and demographic variables are being used to predict for a polychotomous categorical (more than two levels). Multinomial logistic regression is a multivariate test that can yield adjusted odds ratios with 95% confidence intervals.
Recode predictor variables to run multinomial logistic regression in SPSS
SPSS has certain defaults that can complicate the interpretation of statistical findings. When conducting multinomial logistic regression in SPSS, all categorical predictor variables must be "recoded" in order to properly interpret the SPSS output.
For dichotomous categorical predictor variables, and as per the coding schemes used in Research Engineer, researchers have coded the control group or absence of a variable as "0" and the treatment group or presence of a variable as "1."
In order to correctly interpret the SPSS output, the control group will have to be recoded as "1" and the treatment group will have to be recoded as "0."
For polychotomous categorical predictor variables, the recoding becomes a little bit more complicated, but basic numerical logic will yield the correct answer.
As an example, let's say that there is a polychotomous categorical variable with four levels. Researchers have coded "0" as the control group, "1" as the second group, "2" as the third group, and the fourth and final group as "3."
With the defaults in SPSS, this variable will needed to be recoded with "3" as the control group, "2" as the second group, "1" as the third group, and the fourth and final group as "0."
For dichotomous categorical predictor variables, and as per the coding schemes used in Research Engineer, researchers have coded the control group or absence of a variable as "0" and the treatment group or presence of a variable as "1."
In order to correctly interpret the SPSS output, the control group will have to be recoded as "1" and the treatment group will have to be recoded as "0."
For polychotomous categorical predictor variables, the recoding becomes a little bit more complicated, but basic numerical logic will yield the correct answer.
As an example, let's say that there is a polychotomous categorical variable with four levels. Researchers have coded "0" as the control group, "1" as the second group, "2" as the third group, and the fourth and final group as "3."
With the defaults in SPSS, this variable will needed to be recoded with "3" as the control group, "2" as the second group, "1" as the third group, and the fourth and final group as "0."
The steps for conducting a multinomial logistic regression in SPSS
1. The data is entered in a multivariate fashion. The reference category for the polychotomous categorical outcome is codified as "0."
2. Click Analyze.
3. Drag the cursor over the Regression drop-down menu.
4. Click Multinomial Logistic.
5. Click on the polychotomous categorical outcome to highlight it.
6. Click on the arrow to move the variable into the Dependent: box.
7. Click on the Reference Category button.
8. In the Reference Category, click on the First Category marker to select it.
9. Click Continue.
10. Click on the first categorical predictor variable to highlight it.
11. Click on the arrow to move the variable into the Factor(s): box.
12. Repeat Steps 10 and 11 until all of the variables are moved into the Factor(s): box.
13. Click on the first continuous predictor variable to highlight it.
14. Click on the arrow to move the variable into the Covariate(s): box.
15. Repeated Steps 13 and 14 until all of the continuous variables are moved into the Covariate(s): box.
16. Click OK.
2. Click Analyze.
3. Drag the cursor over the Regression drop-down menu.
4. Click Multinomial Logistic.
5. Click on the polychotomous categorical outcome to highlight it.
6. Click on the arrow to move the variable into the Dependent: box.
7. Click on the Reference Category button.
8. In the Reference Category, click on the First Category marker to select it.
9. Click Continue.
10. Click on the first categorical predictor variable to highlight it.
11. Click on the arrow to move the variable into the Factor(s): box.
12. Repeat Steps 10 and 11 until all of the variables are moved into the Factor(s): box.
13. Click on the first continuous predictor variable to highlight it.
14. Click on the arrow to move the variable into the Covariate(s): box.
15. Repeated Steps 13 and 14 until all of the continuous variables are moved into the Covariate(s): box.
16. Click OK.
The steps for interpreting the SPSS output for a multinomial logistic regression
1. Look in the Model Fitting Information table, under the Sig. column. This is the p-value that is interpreted.
If it is LESS THAN .05, then the model fits the data significantly better than the null model. Continue with interpreting the results.
If it is MORE THAN .05, then the model does NOT fit the data better than a model with no parameters in it.
2. Look in the Likelihood Ratio Tests table, in the Sig. column. This is the p-value that is interpreted.
If it is LESS THAN .05, then that variable has a significant overall effect on the outcome.
If it is MORE THAN .05, then that variable does not have a significant overall association with the outcome.
3. Look in the Parameter Estimates table, under the Sig., Exp(B), Lower Bound, and Upper Bound columns. The p-value is in the Sig. column, the adjusted odds ratio is in the Exp(B) column, and the Lower and Upper limits of the 95% confidence interval are presented.
For categorical or ordinal predictors:
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is above 1.0, the risk of the outcome occurring increases that many more times versus the reference category outcome.
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is below 1.0, then the risk of the outcome occurring decreases that many times versus the reference category outcome.
If the p-value is MORE THAN .05, then the 95% CI for the adjusted odds ratio crosses over 1.0 and the association is non-significant.
For continuous predictors:
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is above 1.0, for every one-unit increase in the continuous variable, the risk of the outcome occurring increases that many more times versus the reference category outcome.
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is below 1.0, for every one-unit increase in the continuous variable, the risk of the outcome occurring decreases that many times versus the reference category outcome.
If it is LESS THAN .05, then the model fits the data significantly better than the null model. Continue with interpreting the results.
If it is MORE THAN .05, then the model does NOT fit the data better than a model with no parameters in it.
2. Look in the Likelihood Ratio Tests table, in the Sig. column. This is the p-value that is interpreted.
If it is LESS THAN .05, then that variable has a significant overall effect on the outcome.
If it is MORE THAN .05, then that variable does not have a significant overall association with the outcome.
3. Look in the Parameter Estimates table, under the Sig., Exp(B), Lower Bound, and Upper Bound columns. The p-value is in the Sig. column, the adjusted odds ratio is in the Exp(B) column, and the Lower and Upper limits of the 95% confidence interval are presented.
For categorical or ordinal predictors:
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is above 1.0, the risk of the outcome occurring increases that many more times versus the reference category outcome.
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is below 1.0, then the risk of the outcome occurring decreases that many times versus the reference category outcome.
If the p-value is MORE THAN .05, then the 95% CI for the adjusted odds ratio crosses over 1.0 and the association is non-significant.
For continuous predictors:
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is above 1.0, for every one-unit increase in the continuous variable, the risk of the outcome occurring increases that many more times versus the reference category outcome.
If the p-value is LESS THAN .05 and the adjusted odds ratio with its 95% CI is below 1.0, for every one-unit increase in the continuous variable, the risk of the outcome occurring decreases that many times versus the reference category outcome.
Residuals and multinomial logistic regression
At this point, recode the variables back to their original levels. Then, construct and interpret several plots of the raw and standardized residuals to fully assess model fit. Residuals can be thought of as the error associated with predicting or estimating outcomes using predictor variables. Residual analysis is extremely important for meeting the linearity, normality, and homogeneity of variance assumptions of multinomial logistic regression.
However, it is going to be a tedious process. Take the number of levels of the polychotomous categorical outcome variable, subtract one, and that is the number of times the analysis will have to be performed..
To make this a simple example, let's say that researchers have found a significant main effect using a three-level categorical outcome variable with the reference category outcome codified as "0," with the second level of the outcome = 1, and the last level = 2. REMEMBER TO RECODE YOUR VARIABLES BACK TO THEIR ORIGINAL VALUES!!!
However, it is going to be a tedious process. Take the number of levels of the polychotomous categorical outcome variable, subtract one, and that is the number of times the analysis will have to be performed..
To make this a simple example, let's say that researchers have found a significant main effect using a three-level categorical outcome variable with the reference category outcome codified as "0," with the second level of the outcome = 1, and the last level = 2. REMEMBER TO RECODE YOUR VARIABLES BACK TO THEIR ORIGINAL VALUES!!!
Step 1: Perform a binary logistic regression analysis with reference category outcome = 0 and the next level of the outcome = 1.
Using the aforementioned coding scheme:
1. Click Data.
2. Click Select Cases.
3. In the Select table, click on the If condition is satisfied marker to select it.
4. Click on the If button.
5. Click on the polychotomous categorical outcome variable to highlight it.
6. Click on the arrow to move it into the box.
7. Click the <= button.
8. Type the number, "1"
9. Click Continue.
10. Click OK.
Using the aforementioned coding scheme:
1. Click Data.
2. Click Select Cases.
3. In the Select table, click on the If condition is satisfied marker to select it.
4. Click on the If button.
5. Click on the polychotomous categorical outcome variable to highlight it.
6. Click on the arrow to move it into the box.
7. Click the <= button.
8. Type the number, "1"
9. Click Continue.
10. Click OK.
Step 2: Go to Data View. Researchers will see that only the observations with a "0" or "1" as an outcome are highlighted. Perform a logistic regression analysis on this data. Click on the button to learn how to conduct a logistic regression analysis.
Step 3: Perform the residual analysis for in SPSS:
1. Go back to the Data View. There are three new variables that have been created.
The first is the predicted probability of that observation and is given the variable name of PRE_1.
The second variable contains the raw residuals (the difference between the observed and predicted probabilities of your model) and is given the variable name of RES_1.
The third variable has standardized residuals based on the raw residuals in the second variable and will be given the variable name of as ZRE_1.
2. Click Graphs.
3. Drag the cursor over the Legacy Dialogs drop-down menu.
4. Click Scatter/Dot.
5. Click Simple Scatter to select it.
6. Click Define.
7. Click on the RES_1 or raw residual variable to highlight it.
8. Click on the arrow to move the variable into the Y Axis: box.
9. Click on the PRE_1 or predicted probability variable to highlight it.
10. Click on the arrow to move the variable into the X Axis: box.
11. Click OK.
1. Go back to the Data View. There are three new variables that have been created.
The first is the predicted probability of that observation and is given the variable name of PRE_1.
The second variable contains the raw residuals (the difference between the observed and predicted probabilities of your model) and is given the variable name of RES_1.
The third variable has standardized residuals based on the raw residuals in the second variable and will be given the variable name of as ZRE_1.
2. Click Graphs.
3. Drag the cursor over the Legacy Dialogs drop-down menu.
4. Click Scatter/Dot.
5. Click Simple Scatter to select it.
6. Click Define.
7. Click on the RES_1 or raw residual variable to highlight it.
8. Click on the arrow to move the variable into the Y Axis: box.
9. Click on the PRE_1 or predicted probability variable to highlight it.
10. Click on the arrow to move the variable into the X Axis: box.
11. Click OK.
The steps for interpreting the SPSS scatterplot output with multinomial logistic regression
1. If the points along the scatterplot are symmetric both above and below a straight line, with observations being equally spaced out along the line, then the assumption of linearity can be assumed. Interpretation of these types of scatterplot graphs allows for some subjectivity in regards to symmetry and spread along the line.
If there are significantly larger residuals and wider dispersal of observations along the line, then linearity cannot be assumed.
If there are significantly larger residuals and wider dispersal of observations along the line, then linearity cannot be assumed.
Outliers and multinomial logistic regression
Step 4: Normality and equal variance assumptions apply to logistic regression analyses. Here is how to assess if there are any outliers:
1. Click Analyze.
2. Drag the cursor over the Descriptive Statistics drop-down menu.
3. Click Frequencies.
4. Click on the ZRE_1 or standardized residuals variable to highlight it.
5. Click on the arrow to move the variable into the Variable(s): box.
6. Click OK.
2. Drag the cursor over the Descriptive Statistics drop-down menu.
3. Click Frequencies.
4. Click on the ZRE_1 or standardized residuals variable to highlight it.
5. Click on the arrow to move the variable into the Variable(s): box.
6. Click OK.
Here is how to interpret the SPSS output:
1. Look in the Normalized residual table, under the first column. (It has the word "Valid" in it).
2. Scroll through the entirety of the table.
3. If there are values that are above an absolute value of 2.0, then are outliers.
1. Look in the Normalized residual table, under the first column. (It has the word "Valid" in it).
2. Scroll through the entirety of the table.
3. If there are values that are above an absolute value of 2.0, then are outliers.
Further analyses with multinomial logistic regression
Step 5: Researchers have to conduct this exact same analysis, but with the reference category as "0" and the last level of the outcome = 2.
1. Click Data.
2. Click Select Cases.
3. In the Select table, click on the If condition is satisfied marker to select it.
4. Click on the If button.
5. Clear out the box where the formula goes on the right hand side of the window.
6. Type this: ("Outcome name" = 0) OR ("Outcome name" = 2)
Where "Outcome name" means the variable's name.
7. Click Continue.
8. Click OK.
2. Click Select Cases.
3. In the Select table, click on the If condition is satisfied marker to select it.
4. Click on the If button.
5. Clear out the box where the formula goes on the right hand side of the window.
6. Type this: ("Outcome name" = 0) OR ("Outcome name" = 2)
Where "Outcome name" means the variable's name.
7. Click Continue.
8. Click OK.
Step 6: Go to Data View. Only the observations with a "0" or "2" as an outcome are highlighted. Perform a logistic regression analysis on this data AND all of the subsequent residual analyses. Repeat the individual logistic regression analyses until all of the levels of the polychotomous categorical outcome variable have been compared to the reference category. If all of the models meet the assumptions of linearity, normality, and homogeneity of variance, the overall multinomial model is assumed to fit the data.
Click on the Download Database and Download Data Dictionary buttons for a configured database and data dictionary for multinomial logistic regression. Click on the Validation of Statistical Findings button to learn more about bootstrap, split-group, and jack-knife validation methods.
Statistician For Hire
DO YOU NEED TO HIRE A STATISTICIAN?
Eric Heidel, Ph.D. will provide statistical consulting for your research study at $100/hour. Secure checkout is available with PayPal, Stripe, Venmo, and Zelle.
- Statistical Analysis
- Sample Size Calculations
- Diagnostic Testing and Epidemiological Calculations
- Psychometrics