Incremental validity
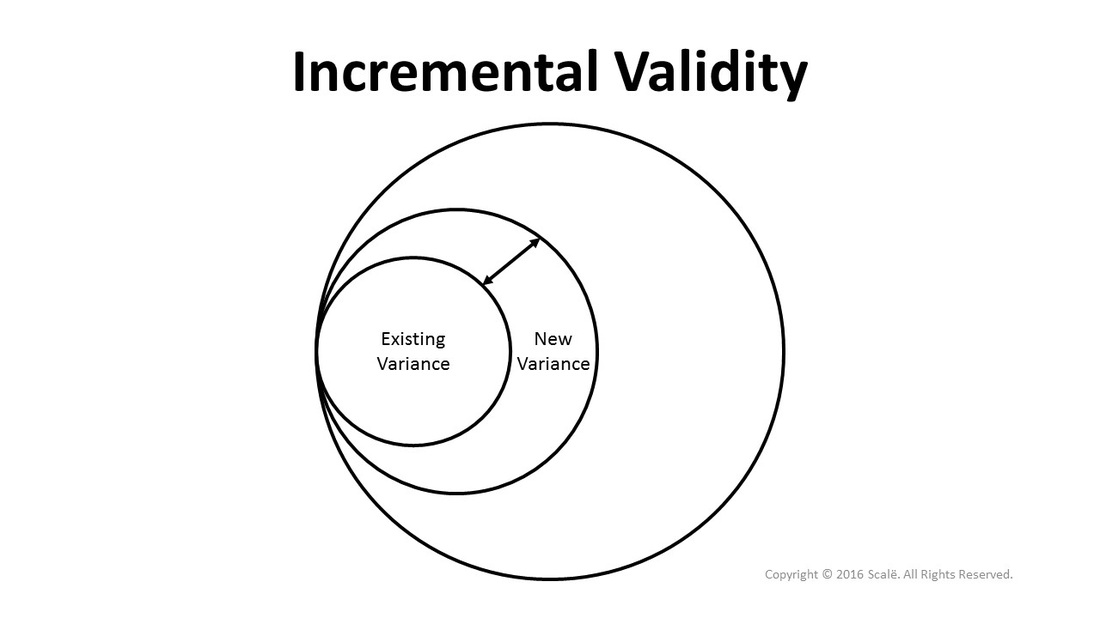
Account for new and unique variance in a construct or body of knowledge
Incremental validity is the ability of a survey score to add new and unique variance to a theoretical or conceptual framework.
Stepwise regression techniques are used to assess if the introduction of the composite or subscale scores of a survey into a multivariate model comprised of other similar surveys will increase the amount of variance accounted for in the outcome variable. If the F-test finds a significant increase in shared variance as result of your survey score entering a model, then evidence of incremental validity is assumed.
Stepwise regression techniques are used to assess if the introduction of the composite or subscale scores of a survey into a multivariate model comprised of other similar surveys will increase the amount of variance accounted for in the outcome variable. If the F-test finds a significant increase in shared variance as result of your survey score entering a model, then evidence of incremental validity is assumed.
The steps for conducting stepwise regression in SPSS
1. The data is entered in a multivariate fashion.
2. Click Analyze.
3. Drag the cursor over the Regression drop-down menu.
4. Click Linear.
5. Click on the continuous outcome variable to highlight it.
6. Click on the arrow to move the variable into the Dependent: box.
7. Click on the first predictor variable to highlight it.
8. Click on the arrow to move the variable into the Independent(s): box.
9. Repeat Steps 7 and 8 until all of the predictor variables are in the Independent(s): box.
10. Click on the Statistics button.
11. Click on the R squared change, Collinearity diagnostics, Durbin-Watson, and Casewise diagnostics boxes to select them.
12. Click on the Plots button.
13. Click on the DEPENDNT variable to highlight it.
14. Click on the arrow to move the variable into the X: box.
15. Click on the *ZRESID variable to highlight it.
16. Click on the arrow to move the variable into the Y: box.
17. In the Standardized Residual Plots table, click on the Histogram and Normal probability plot boxes to select them.
18. Click Continue.
19. Click on the Method: drop-down menu.
20. Click on Stepwise.
21. Click OK.
2. Click Analyze.
3. Drag the cursor over the Regression drop-down menu.
4. Click Linear.
5. Click on the continuous outcome variable to highlight it.
6. Click on the arrow to move the variable into the Dependent: box.
7. Click on the first predictor variable to highlight it.
8. Click on the arrow to move the variable into the Independent(s): box.
9. Repeat Steps 7 and 8 until all of the predictor variables are in the Independent(s): box.
10. Click on the Statistics button.
11. Click on the R squared change, Collinearity diagnostics, Durbin-Watson, and Casewise diagnostics boxes to select them.
12. Click on the Plots button.
13. Click on the DEPENDNT variable to highlight it.
14. Click on the arrow to move the variable into the X: box.
15. Click on the *ZRESID variable to highlight it.
16. Click on the arrow to move the variable into the Y: box.
17. In the Standardized Residual Plots table, click on the Histogram and Normal probability plot boxes to select them.
18. Click Continue.
19. Click on the Method: drop-down menu.
20. Click on Stepwise.
21. Click OK.
The steps for interpreting the SPSS output for stepwise regression
1. Look in the Model Summary table, under the R Square and the Sig. F Change columns. These are the values that will be interpreted.
The R Square value is the amount of variance in the outcome that is accounted for by the predictor variables researchers have used.
If the p-value is LESS THAN .05, the model has accounted for a statistically significant amount of variance in the outcome.
If the p-value is MORE THAN .05, the model has not accounted for a significant amount of the outcome.
2. Look in the Coefficients table, under the B, Std. Error, Beta, Sig., and Tolerance columns.
The B column contains the unstandardized beta coefficients that depict the magnitude and direction of the effect on the outcome variable.
The Std. Error contains the error values associated with the unstandardized beta coefficients.
The Beta column presents unstandardized beta coefficients for each predictor variable.
The Sig. column shows the p-value associated with each predictor variable.
If a p-value is LESS THAN .05, then that variable has a significant association with the outcome variable.
If a p-value is MORE THAN .05, then that variable does not have a significant association with the outcome variable.
The Tolerance column presents values related to assessing multicollinearity amongst the predictor variables.
If any of the Tolerance values are BELOW .75, consider creating a new variable or deleting one of the predictor variables.
The R Square value is the amount of variance in the outcome that is accounted for by the predictor variables researchers have used.
If the p-value is LESS THAN .05, the model has accounted for a statistically significant amount of variance in the outcome.
If the p-value is MORE THAN .05, the model has not accounted for a significant amount of the outcome.
2. Look in the Coefficients table, under the B, Std. Error, Beta, Sig., and Tolerance columns.
The B column contains the unstandardized beta coefficients that depict the magnitude and direction of the effect on the outcome variable.
The Std. Error contains the error values associated with the unstandardized beta coefficients.
The Beta column presents unstandardized beta coefficients for each predictor variable.
The Sig. column shows the p-value associated with each predictor variable.
If a p-value is LESS THAN .05, then that variable has a significant association with the outcome variable.
If a p-value is MORE THAN .05, then that variable does not have a significant association with the outcome variable.
The Tolerance column presents values related to assessing multicollinearity amongst the predictor variables.
If any of the Tolerance values are BELOW .75, consider creating a new variable or deleting one of the predictor variables.
Residuals
At this point, researchers need to construct and interpret several plots of the raw and standardized residuals to fully assess the fit of the model. Residuals can be thought of as the error associated with predicting or estimating outcomes using predictor variables. Residual analysis is extremely important for meeting the linearity, normality, and homogeneity of variance assumptions of multiple regression.
Scroll down the bottom of the SPSS output to the Scatterplot. If the plot is linear, then researchers can assume having met the assumption of linearity.
Scroll down the bottom of the SPSS output to the Scatterplot. If the plot is linear, then researchers can assume having met the assumption of linearity.
Outliers
Normality and equal variance assumptions also apply to multiple regression analyses.
Look at the P-P Plot of Regression Standardized Residual graph. If there are not significant deviations of residuals from the line and the line is not curved, then normality and homogeneity of variance can be assumed.
Look at the P-P Plot of Regression Standardized Residual graph. If there are not significant deviations of residuals from the line and the line is not curved, then normality and homogeneity of variance can be assumed.
Click on a button below to continue.
Statistician For Hire
DO YOU NEED TO HIRE A STATISTICIAN?
Eric Heidel, Ph.D. will provide statistical consulting for your research study at $100/hour. Secure checkout is available with PayPal, Stripe, Venmo, and Zelle.
- Statistical Analysis
- Sample Size Calculations
- Diagnostic Testing and Epidemiological Calculations
- Psychometrics