Statistical power and small sample sizes
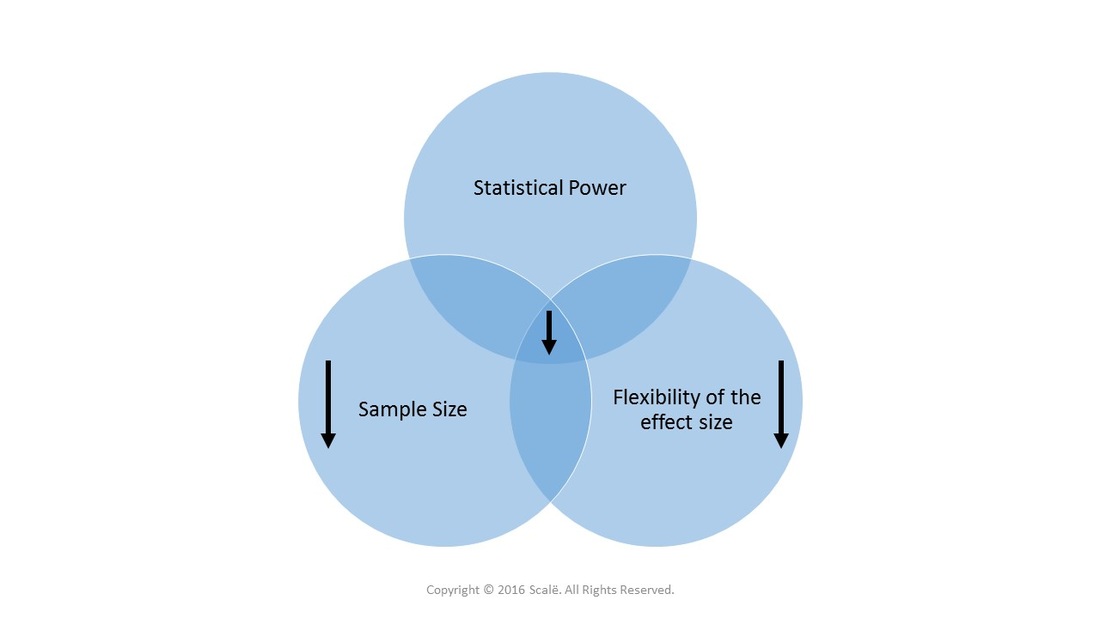
Small sample sizes decrease statistical power and decrease the flexibility of the effect size
Statistically significant findings are harder to detect with small sample sizes. This means that small sample sizes decrease statistical power. Finding non-significant differences with small sample sizes often leads to committing Type II errors. There is not as much flexibility of effects size (ability to detect both small and large effect sizes, regardless of limited or extensive variance) with small sample sizes.
Significant effects with small sample sizes are easier to detect when using within-subjects designs and continuous level outcomes. Small sample sizes are not robust enough for between-subjects and multivariate designs, or when measuring for categorical and ordinal outcomes.
Significant effects with small sample sizes are easier to detect when using within-subjects designs and continuous level outcomes. Small sample sizes are not robust enough for between-subjects and multivariate designs, or when measuring for categorical and ordinal outcomes.
Small sample sizes decrease statistical power and decrease the flexibility of effect sizes.
Click on the Sample Size button below to continue.
Hire A Statistician
DO YOU NEED TO HIRE A STATISTICIAN?
Eric Heidel, Ph.D., PStat will provide the following statistical consulting services for undergraduate and graduate students at $100/hour. Secure checkout is available with Stripe, Venmo, Zelle, or PayPal.
- Statistical Analysis
- Research Design
- Sample Size Calculations
- Diagnostic Testing and Epidemiological Calculations
- Survey Design and Psychometrics