Sensitivity

Sensitivity is about detecting disease with a diagnostic test

Sensitivity measures the ability of a diagnostic test to detect a disease state.  In order to set up an experiment to calculate the sensitivity of a diagnostic test, researchers must have a current "gold standard" diagnostic test to use as a reference. 
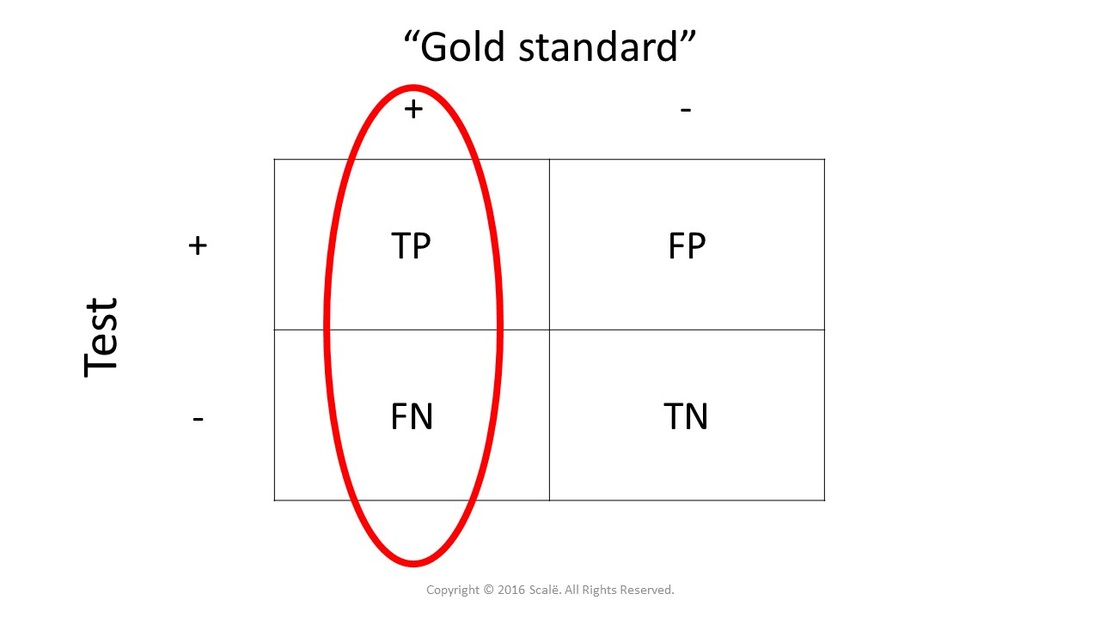
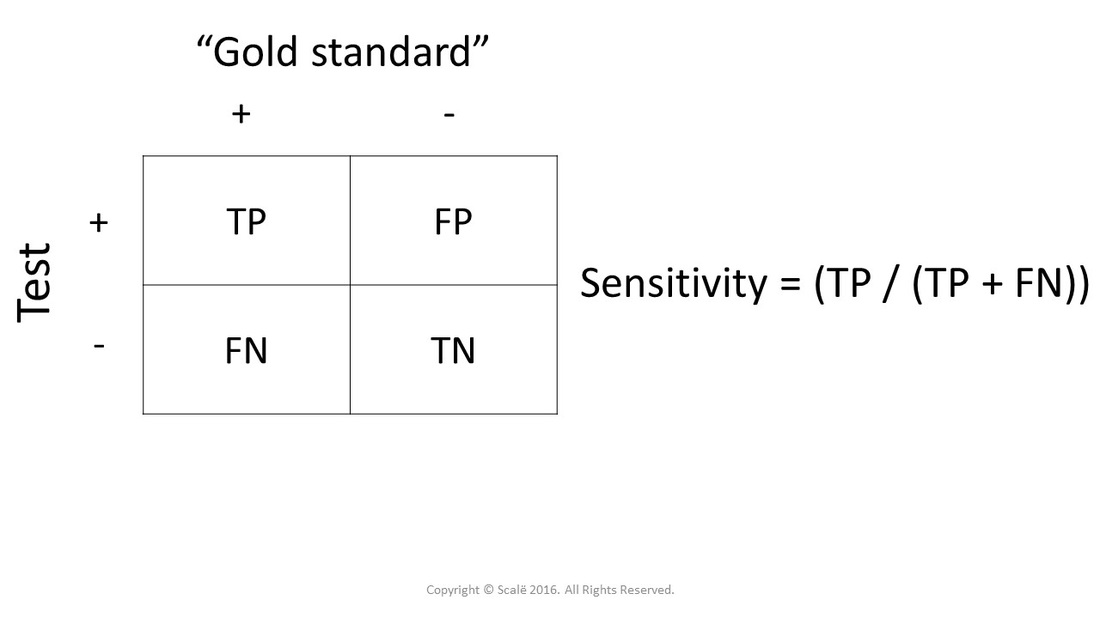
In the 2X2 table, sensitivity is calculated using these values:
Sensitivity is focused on the participants that tested positive with the
Sensitivity is the number of people with a disease (as rated by the "gold standard") that have positive test results for the diagnostic test. In other words, sensitivity is the proportion of people that had the disease and tested positive for the diagnostic test.

Another interesting aspect of sensitivity is that in some cases, it can "rule out" a given disease state. If a test has high sensitivity (> 95%), then it can detect disease. This means, at the same time, that a negative test result is a strong indication that a person does NOT have the disease.  With high sensitivity, the ability to "rule out" disease states will increase.
Here is a 2X2 table depicting the calculation of sensitivity:  
Sensitivity is the ability of a diagnostic test to detect disease states.
Sensitivity
There is a quick and easy calculation that shows if a diagnostic test is useful in any capacity whatsoever, the Youden index. The formula is ((Sensitivity + Specificity) - 100). Any Youden index value below 50% means that test is essentially worthless and should be discarded. 
Click on the Specificity button to continue.
Specificity
Back to Diagnostic Testing
Research Engineer Home Page

Statistician For Hire

$100.00
Buy Now

DO YOU NEED TO HIRE A STATISTICIAN?

Eric Heidel, Ph.D. will provide statistical consulting for your research study at $100/hour. Secure checkout is available with PayPal, Stripe, Venmo, and Zelle.

  • Statistical Analysis
  • Sample Size Calculations
  • Diagnostic Testing and Epidemiological Calculations
  • Psychometrics