Fixed-effects ANOVA
Test interactions between multiple categorical variables
Fixed-effects ANOVA is used to answer research questions where the variance across different levels of multiple categorical variables is assessed. Many times with fixed-effects ANOVA, there are demographic, prognostic, and clinical variables that confound and mitigate associations between predictor and outcome variables. Fixed-effects ANOVA allows you to answer these more complex research questions, and thus, generate evidence that is more indicative of the outcome as it truly exists in the population of interest. The fixed-effects ANOVA focuses on how a continuous outcome varies across "fixed" factors of two or more categorical predictor variables.
For example, let's say researchers are interested in the effects of gender (male versus female) and exposure to a new marketing concept (exposure versus non-exposure) in relation to how many units of a product that a person will purchase (number of units). Gender and exposure are "fixed" effects in that each participant is forced into one of the categories for each subsequent variable. Therefore, researchers can assess the average number of units that different types of people will purchase. Researchers will be able to compare the mean number of units purchased by 1) males exposed to the marketing, 2) females exposed to the marketing, 3) males not exposed to the marketing, and 4) females not exposed to the marketing.
The marginal means and errors for each level of the interaction should be presented. Significant main effects must be further tested in a post hoc fashion to assess where amongst the levels of the interaction the significance exists and and when either of the "fixed" effects is polychotomous (more than two "fixed" levels of a variable).
For example, let's say researchers are interested in the effects of gender (male versus female) and exposure to a new marketing concept (exposure versus non-exposure) in relation to how many units of a product that a person will purchase (number of units). Gender and exposure are "fixed" effects in that each participant is forced into one of the categories for each subsequent variable. Therefore, researchers can assess the average number of units that different types of people will purchase. Researchers will be able to compare the mean number of units purchased by 1) males exposed to the marketing, 2) females exposed to the marketing, 3) males not exposed to the marketing, and 4) females not exposed to the marketing.
The marginal means and errors for each level of the interaction should be presented. Significant main effects must be further tested in a post hoc fashion to assess where amongst the levels of the interaction the significance exists and and when either of the "fixed" effects is polychotomous (more than two "fixed" levels of a variable).
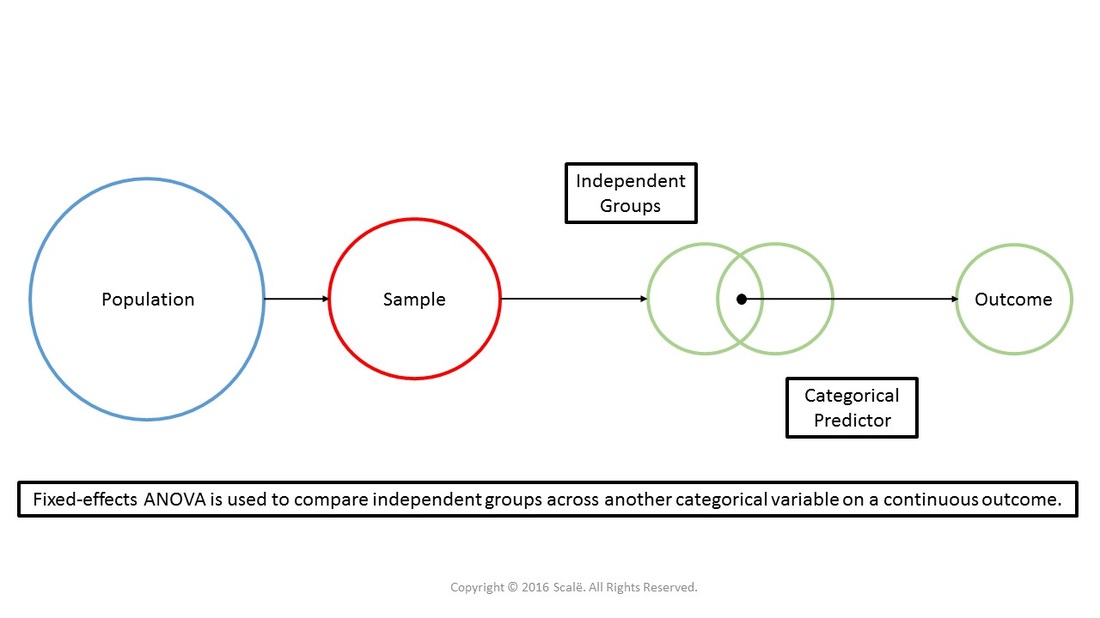
The figure below depicts the use of fixed-effects ANOVA. Independent groups are being compared across the levels of another categorical variable on a continuous outcome. Fixed-effects ANOVA is used to understand the interaction between two categorical variables on a continuous outcome. Marginal means and standard errors are yielded from fixed-effects ANOVA.
The steps for conducting a fixed-effects ANOVA in SPSS
1. The data is entered in a between-subjects fashion.
2. Click Analyze.
3. Drag the cursor over the General Linear Model drop-down menu.
4. Click Univariate.
5. Click on the continuous outcome variable to highlight it.
6. Click on the arrow to move the variable into the Dependent Variable: box.
7. Click on the first categorical "factor" variable to highlight it.
8. Click on the arrow to move the variable into the Fixed Factor(s): box.
9. Click on the second categorical "factor" variable to highlight it.
10. Click on the arrow to move the variable into the Fixed Factor(s): box.
11. Click on the Plots button.
12. Click on the grouping or first "factor" variable to highlight it.
13. Click on the arrow to move the variable into the Separate Lines: box.
14. Click on the second "factor" variable to highlight it.
15. Click on the arrow to move the variable into the Horizontal Axis: box.
16. Click on the Add button.
17. Click Continue.
18. Click the Options button.
19. In the Estimated Marginal Means table, in the Factor(s) and Factor Interactions: box, click on the first "factor" variable to highlight it.
20. Click on the arrow to move the variable into the Display Means for: box.
21. Repeat Steps 19 and 20 for all "factor" variables and the interaction effect denoted as first "factor"*second "factor."
22. Click on the Compare main effects box to select it.
23. In the Display table, click on the Descriptive statistics, Estimates of effect size, Observed power, and Homogeneity tests boxes to select them.
24. Click Continue.
25. Click OK.
2. Click Analyze.
3. Drag the cursor over the General Linear Model drop-down menu.
4. Click Univariate.
5. Click on the continuous outcome variable to highlight it.
6. Click on the arrow to move the variable into the Dependent Variable: box.
7. Click on the first categorical "factor" variable to highlight it.
8. Click on the arrow to move the variable into the Fixed Factor(s): box.
9. Click on the second categorical "factor" variable to highlight it.
10. Click on the arrow to move the variable into the Fixed Factor(s): box.
11. Click on the Plots button.
12. Click on the grouping or first "factor" variable to highlight it.
13. Click on the arrow to move the variable into the Separate Lines: box.
14. Click on the second "factor" variable to highlight it.
15. Click on the arrow to move the variable into the Horizontal Axis: box.
16. Click on the Add button.
17. Click Continue.
18. Click the Options button.
19. In the Estimated Marginal Means table, in the Factor(s) and Factor Interactions: box, click on the first "factor" variable to highlight it.
20. Click on the arrow to move the variable into the Display Means for: box.
21. Repeat Steps 19 and 20 for all "factor" variables and the interaction effect denoted as first "factor"*second "factor."
22. Click on the Compare main effects box to select it.
23. In the Display table, click on the Descriptive statistics, Estimates of effect size, Observed power, and Homogeneity tests boxes to select them.
24. Click Continue.
25. Click OK.
The steps for interpreting the SPSS output for a fixed-effects ANOVA
1. Look in the Tests of Between-Subjects Effects, under the Sig. column. These are the p-values that are interpreted. Researchers want to focus specifically on the p-values for the two "factors" and the interaction.
If a p-value is LESS THAN .05 for one or both of the "factors," this means that there is a statistically significant difference between the independent groups or levels of the categorical variable.
If a p-value is MORE THAN .05 for one or both of the "factors," this means that there is NOT a statistically significant difference between the independent groups or levels of the categorical variable.
2. Researchers are running this statistic to see if these two "factor" variables account for more of the variance in the continuous outcome variable when put together versus when they are assessed in a mutually exclusive (univariate) fashion. The interaction effect tests to see if the continuous outcome is different across levels of the first "factor" and second "factor" concurrently.
For example, imagine that researchers want to know if there is a difference between men and women who are <40 years old compared to those >40 years old on how they rate the taste of a new product. This means that there are four (4) different groups that are being compared in a "factorial" manner: 1) Men that are <40 years old, 2) women that are <40 years old, 3) men that are >40 years old, and 4) women that are >40 years old. These four group means and standard deviations are being compared using the fixed-effects ANOVA.
If the interaction p-value is LESS THAN .05, then researchers have evidence of a significant main interaction effect, meaning that there is some sort of difference going on among the four groups (just like the main effect of an ANOVA).
If the interaction p-value is MORE THAN .05, then there is NOT a significant difference amongst the four groups and no interaction between the two "factor" variables.
3. If any of the "factors" or the interaction had a p-value LESS THAN .05, scroll down to the Estimated Marginal Means section of the SPSS output. Researchers will see the "factor" variable names with tables underneath them.
The first table, Estimates, has the mean and standard error with 95% CIs of the mean for each level of the "factor" variable.
The second table, Pairwise Comparisons, has the p-values associated with comparing each independent group or level of the categorical "factor" variable. These tests are similar to the post hoc tests run in regular ANOVAs. Researchers have to explain where among the independent groups or levels of the "factor" that the differences exist.
If a p-value in the Sig. column of the Pairwise Comparisons table is LESS THAN .05, then researchers have evidence of a statistically significant difference between the independent groups or levels of the "factor" variable.
if a p-value in the Sig. column of the Pairwise Comparisons table is MORE THAN .05, then researchers do NOT have evidence of a statistically significant difference between the independent groups or levels of the "factor" variable.
4. Finally, look at the last table entitled "Factor 1"*"Factor 2." These are the marginal means of the interaction effect that researchers are testing for with the factorial ANOVA. If the p-value associated with the interaction was significant back up in the Between-Subjects Effects table, then these are the means associated with that significant interaction. It shows how the four groups differed in regards to their means.
From the example above, it would show how men and women of different age groups differed on how they rated the taste of the product. The researchers would then have evidence that could inform upon targeting advertisements to consumers in the marketplace.
5. Look at the graph for a visual depiction of the interaction effect. The means for all four groups are plotted.
If a p-value is LESS THAN .05 for one or both of the "factors," this means that there is a statistically significant difference between the independent groups or levels of the categorical variable.
If a p-value is MORE THAN .05 for one or both of the "factors," this means that there is NOT a statistically significant difference between the independent groups or levels of the categorical variable.
2. Researchers are running this statistic to see if these two "factor" variables account for more of the variance in the continuous outcome variable when put together versus when they are assessed in a mutually exclusive (univariate) fashion. The interaction effect tests to see if the continuous outcome is different across levels of the first "factor" and second "factor" concurrently.
For example, imagine that researchers want to know if there is a difference between men and women who are <40 years old compared to those >40 years old on how they rate the taste of a new product. This means that there are four (4) different groups that are being compared in a "factorial" manner: 1) Men that are <40 years old, 2) women that are <40 years old, 3) men that are >40 years old, and 4) women that are >40 years old. These four group means and standard deviations are being compared using the fixed-effects ANOVA.
If the interaction p-value is LESS THAN .05, then researchers have evidence of a significant main interaction effect, meaning that there is some sort of difference going on among the four groups (just like the main effect of an ANOVA).
If the interaction p-value is MORE THAN .05, then there is NOT a significant difference amongst the four groups and no interaction between the two "factor" variables.
3. If any of the "factors" or the interaction had a p-value LESS THAN .05, scroll down to the Estimated Marginal Means section of the SPSS output. Researchers will see the "factor" variable names with tables underneath them.
The first table, Estimates, has the mean and standard error with 95% CIs of the mean for each level of the "factor" variable.
The second table, Pairwise Comparisons, has the p-values associated with comparing each independent group or level of the categorical "factor" variable. These tests are similar to the post hoc tests run in regular ANOVAs. Researchers have to explain where among the independent groups or levels of the "factor" that the differences exist.
If a p-value in the Sig. column of the Pairwise Comparisons table is LESS THAN .05, then researchers have evidence of a statistically significant difference between the independent groups or levels of the "factor" variable.
if a p-value in the Sig. column of the Pairwise Comparisons table is MORE THAN .05, then researchers do NOT have evidence of a statistically significant difference between the independent groups or levels of the "factor" variable.
4. Finally, look at the last table entitled "Factor 1"*"Factor 2." These are the marginal means of the interaction effect that researchers are testing for with the factorial ANOVA. If the p-value associated with the interaction was significant back up in the Between-Subjects Effects table, then these are the means associated with that significant interaction. It shows how the four groups differed in regards to their means.
From the example above, it would show how men and women of different age groups differed on how they rated the taste of the product. The researchers would then have evidence that could inform upon targeting advertisements to consumers in the marketplace.
5. Look at the graph for a visual depiction of the interaction effect. The means for all four groups are plotted.
The above stated methods and output relates to a simple 2x2 factorial design. A fixed effects ANOVA can be run on categorical variables with more than two independent groups or levels of a "factor." For instance, if researchers wanted to compare 1) young adults from the Southeastern United States, Pacific Northwest, and Midwest that have a salary 2) less than $30,000 a year, a salary between $30,001 - $50,000 a year, and a salary of $50,001 or more a year, then theu would have a 3 (SE US, PN US, MW US) X 3 (<$30,000, $30,001-$50,000, >%50,000) factorial ANOVA with nine different independent group means being compared.
Click on the Download Database and Download Data Dictionary buttons for a configured database and data dictionary for fixed-effects ANOVA. Click on the Validation of Statistical Findings button to learn more about bootstrap, split-group, and jack-knife validation methods.
Statistician For Hire
DO YOU NEED TO HIRE A STATISTICIAN?
Eric Heidel, Ph.D. will provide statistical consulting for your research study at $100/hour. Secure checkout is available with PayPal, Stripe, Venmo, and Zelle.
- Statistical Analysis
- Sample Size Calculations
- Diagnostic Testing and Epidemiological Calculations
- Psychometrics